Основной базой для всех учений, познающих мир, является математика. Точная наука использует формализованный язык и изучает порядок, структуру и отношения на выбранных абстрактных объектах. Не всем обучающимся нравится математика из-за её сложности и запутанности, а, скорее всего, из-за непонимания. Прочные изменения в отношении к математике потребуют увлеченности, сосредоточенности, последовательности, даже упрямства и, главное, практических решений. В изучении важно шаг за шагом разбираться изначально в простом и постепенно переходить к более сложному, не оставляя непонятного и непродуманного.
Существуют много различных разделов математики уже достаточно изученных и появившихся недавно. Далее рассказывается об азах математического анализа – основных начальных понятиях, определениях и правилах исследования простых функций одной переменной, производной и дифференцирования.
У студентов начальных курсов вузов появился афоризм: «Математика становится по-настоящему сложной, когда из неё пропадают цифры». И действительно, к пониманию некоторых определений и законов математической науки приближаются путем решения по правилам на конкретных примерах.
Основные определения
Начнем с терминологии – с простых общих смысловых значений первичных определений:
- Переменная – величина или символ, может принимать любое из ряда значений в
определенной области (вес или рост ребенка)
- Функция – назначение, работа, деятельность, определенное действие над переменной, обозначим f(x) (зависимость веса ребенка от его роста)
- Предел – лимит, граница, край (горизонт – граница обзора)
- Производная – образованная, вторичная, проистекшая от другого, обозначим f’(x) (скорость при движении)
- Дифференциал – разность, различие, разделение.
Функция это просто
Функция – это результат того, что она делает с переменной, что является итогом вычисления. Это взаимосвязь элементов, при которой изменение одного переменного обуславливает изменение в другом. Разделяют f(x) на простые и сложные.
Для отображения зависимостей используются следующие способы: алгебраический, графический, табличный, логический и даже программные.
Определяют числовые зависимости алгебраически с использованием символов переменных, равенств и неравенств (≤ и >), строится уравнение вида: y = f(x), здесь x — переменная или аргумент, а y или f(x) — функция. Каждому конкретному значению переменной x из допустимой области определения соответствует определенное значение y для заданной f (x).
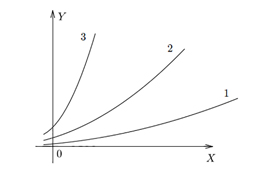
На рисунке ниже представлены простые графики 3-х различных соотношений. Видно, что в f(x) 3 получается наибольшее значение y при х конкретном, в f(x) 1 — наименьшее.
Функция
Различают следующие элементарные выражения: линейная (прямая), квадратичная (парабола), кубическая, гипербола, показательная, логарифмическая, тригонометрические (приведены в таблице ниже).
Для анализа каждого вида f(x) определяют присущие им свойства (перечислены ниже), для этого используют понятия производной и дифференциала.
Производная функции
Производная – оператор, который для исходной f(x) по законам дифференцирования ставит в соответствие другую функцию, она характеризует изменение первичной f(x) аргумента x в некоторой точке. Для её детального понимания следует разобраться с более сложными определениями предела зависимости и дифференцирования.
Предел – это определение динамическое. Выражение, что x стремится к n, понимают так – х обретает значения, которые близко приближаются к п и разнятся на мизерную величину.
Дифференциал – малое изменение какой-то величины. Приращение назовем дельтой.
Производной для f(x) в точке является предел деления дельты функции к дельте переменной в данной точке, если последняя стремится к 0.
Характеристика скорости изменения зависимости в данной точке, геометрически её можно показать, как значение tg угла наклона альфа касательной к функции.
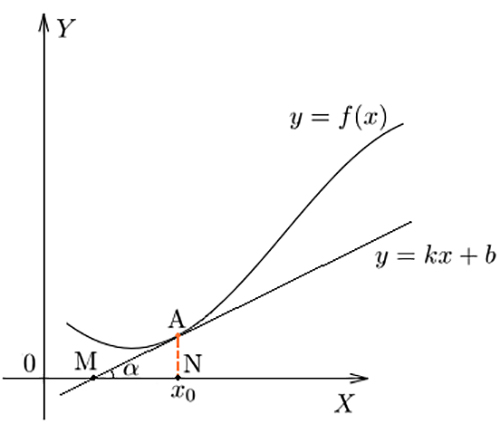
Производная
Зависимость называется дифференцируемой, если определена f’(x). Нахождение производной называется дифференцированием. Правила вычисления f’(x) и соответствия f’(x) от элементарных f(x) приведены в таблице ниже
Производная функции также функция
Каждая зависимость имеет определенные свойства, зная и исследуя их можно анализировать характер состояния и изменения f(x).
Основные свойства:
- Данные промежутков определений и промежутков значений.
- Нулевые значения f(x)
- Функция возрастает или убывает в некоторых промежутках.
- Точки MAX и MIN функции, есть ли перегиб.
- Четная или нечетная f(x)
- Ограниченная и неограниченная функция.
- Есть ли асимптоты.
- Периодичность f(x).

Функции и производные
При установлении характеристик зависимости с помощью производной используют взаимосвязи свойств f’(x) со свойствами f(x) и наоборот. На графике функции легко определяются характеристики f’(x), и наоборот по графику f’(x) понимаются характеристики первичной f(x). Фиксируя сущность каждой особенности функции, исследуют и устанавливают цепочку связей. Для определения асимптот в графиках используют понятие пределов.
Ниже приведены некоторые характеристики и зависимости f’(x) от f(x):
- При возрастании f(x) на промежутке, f’(x) положительна.
- В случае убывания f(x) на промежутке, f’(x) отрицательна.
- При наличии f(x) точки MAX, в ней f’(x)=0 может не определена, и tg угла касательной меняет знак с + на -.
- При наличии f(x) точки MIN, в ней f’(x)=0 может не определена, и tg угла касательной меняет знак с – на +.
- При перегибе в Е графика f(x) значение f’(x) не поменяло в точке знак, f’(x)=0.
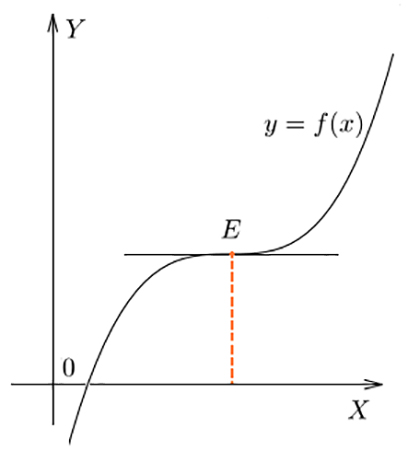
Перегиб в точке Е графика функции
Для исследования f(x) составляют схему, где каждый шаг строится по определенному алгоритму вычислений и анализа взаимосвязей составляющих элементов.
Различия функции и производной
Правила сложения и вычитания f(x) одинаковы с правилами этих действий при дифференцировании. Но правила нахождения f’(x) при действиях умножения и деления функций другие (как в таблице).
Функция первична, а производная – произведенная вторичная математическая операция, у них в большинстве случаев разные характеристики.
Точку перегиба непрерывной зависимости находят по её второй производной, должен меняться её знак в районе точки х0.
Есть такие типы функций не имеющих f’(x) в точке x0 (разрывные). В выражении ln(|x|-1) не определена в точке x0=1 производная.
Есть выражения «по модулю» аналогичные y=|x|, которые имеет излом в х0.
Для подобных зависимостей применяются лишь частично (на промежутках области определения) способы исследования их свойств с помощью производных и не всегда возможен переход от свойств f’(x) к свойствам первичной.
Нигде не обойтись без исключений из правил, и даже в математике. С целью разбора и закрепления изложенного материала обязательно следует порешать примеры, напрактиковаться, набраться опыта с пределами, дифференциалами и производными и смело переходить к интегралам.