Для подведения статистики применяется множество формул, определений и терминов. Они позволяют точно оценить большой объем данных, например, доходы и расходы предприятий за длительный период времени. В статистике наиболее часто используются понятия среднее арифметическое значение и медиана. Эти 2 определения чаще всего применяются вместе, чтобы выводы были более точными. Однако в общественных структурах чаще используется только среднее арифметическое.
Медиана
Этот термин используется в математике (геометрии), статистике, экономике, политике и других сферах деятельности. В статистических отсчетах определение характеризует набор множеств (специалисты часто называют его выборкой). Это данные, состоящие из множества неравных чисел.

Медиана — это одно множество, стоящее в середине. Она делит всю последовательность на 2 одинаковые части:
- Данные, меньшие значения.
- Данные, большие значения.
Все множества сортируются по возрастанию. Точное значение вычисляется при нечетном количестве элементов совокупности.
Если последовательность состоит из четного количества значений, переменная может быть определена неоднозначно. В таком случае суммируют 2 соседних числа, и делят сумму на 2.
Главные свойства характеристики:
- Не зависит от элементов, расположенных справа и слева от нее.
- При объединении нескольких последовательностей (с известными размерностями), невозможно сразу определить итоговую характеристику.
- Минимальное отличие от абсолютных отклонений, по сравнению с другими статистическими терминами.
- Чем меньше отклонения у чисел совокупности, тем ближе они к значению термина.
Среднее арифметическое
Эта размерность является основной в математике (алгебре) и статистике. Она вычисляется по формуле: сумма всех элементов последовательности, деленная на количество.
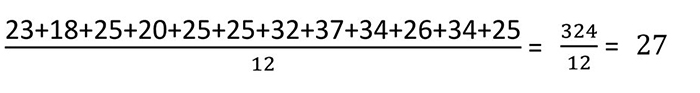
Определение используют для обработки сведений за большой период времени. Оно применимо для политической, экономической и социальной сфер. Ее часто используют, как показатель нескольких вычислений или сбора данных.
Многие статисты считают его неэффективным, так как множество лучше применяется для меньшей последовательности. Оно не показывает максимум и минимум, если они кардинально отличаются, а совокупность данных большая. К другим недостаткам характеристики относятся:
- Подвергается влиянию чрезмерных отклонений (если данные отличаются на большие числа).
- Показывает неправильные данные при измерении сведений циклических переменных (вычисление угла наклона или фазы события).
- Плохо применяется к вычислению процентных величин (подсчет инвестиций).
Общая характеристика
Оба статистических термина применяются для обработки данных, выявления статистики и подведения итогов. В частных случаях данные переменные могут иметь равные значения.
Терминами пользуются в разных научных сферах, например в математике. Среднее арифметическое имеет в алгебре и статистике одинаковые определение и формулы. Медиана в математике применяется в геометрии — это отрезок, проведенный из угла треугольника к противолежащей этому углу стороне, и делящий сторону на 2 равных отрезка.
Для подробной статистики используются одновременно оба термина, вместе с другими переменными (мода, частота, выбросы и пр.). Это позволяет более точно оценить собранные данные о подсчетах доходов и расходов, измерениях температуры, объема воды и др.
Если все числа совокупности равны, то числа переменных будут равными и равны всем элементам последовательности.
Отличия определений
Формулировка и определение
Медиана делит последовательность пополам, причем 1 часть состоит из элементов, меньших этой величины, а 2 часть состоит из больших чисел. Среднее арифметическое — это сумма всех элементов, деленная на их количество.
Данные в некоторых случаях совпадают, однако чаще всего они имеют разные значения.
Точность вычислений
Среднее арифметическое дает неточный итог подведения статистики, особенно если данных слишком много. Некоторые статисты заменяют его модой — элемент, который чаще всего встречается в последовательности. В частных случаях необходимо использовать среднее геометрическое, так как арифметическое дает неточный результат. Оценить эффективность величины можно только после применения его на практике, изучения всех значений последовательности и вычисления других статистических характеристик.
Медиана является более точной величиной, чем другое множество.
Однако для эффективной статистики необходимо учитывать сразу несколько показателей.
Применение
Для большинства обывателей медиана — это не статистическая величина, а математическая. Она чаще применяется в геометрических задачах на треугольники, как отрезок или луч. Многие даже не знают, что данное определение применимо к статистике. Его используют только при специализированных отчетах, для подведения итога. В устных докладах переменную не озвучивают, однако в документации ее необходимо описывать.
Среднее арифметическое также применяется в математике, однако в статистике оно известно не меньше. Его часто используют в СМИ, политике и экономике. Эта переменная изучается на начальной стадии обучения статистике.
Для большинства обывателей среднее арифметическое — более понятная величина, несмотря на то, что она неточна во многих случаях.