Чем отличается определенный интеграл от неопределенного

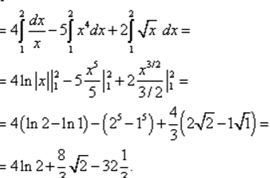
Сегодня слово «Интеграл» можно услышать довольно часто, причем, зачастую, в самых неожиданных местах, например на биржевом канале по телевизору, или по новостям. Нередко мы слышим словосочетание «интегральные показатели» , слово «интегрированный», «интегративный» и тому подобное. Ну, по большому счету, чиновники и телеведущие, вообще, очень любят разные умные слова, правда вряд ли они понимают их истинное значение. А мы сегодня поговорим о том, что же такое интеграл, какие виды интеграла существуют и в чем их отличия.

Что такое интеграл

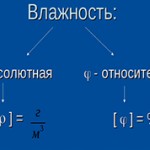
Интеграл- это латинское слово, которое пришло к нам из античности, и означает оно «Целый», или «Полный». То есть, ясно, что если про некий объект, например, сосуд молока говорили «интегер», это означало, что он полный, и молока в нем сколько было, столько и осталось.

Со временем это слово стали употреблять в совершенно разных дисциплинах- в философии, политике, экономике, в алгебре и геометрии. Но наиболее простую интерпретацию интегралу дает математика.

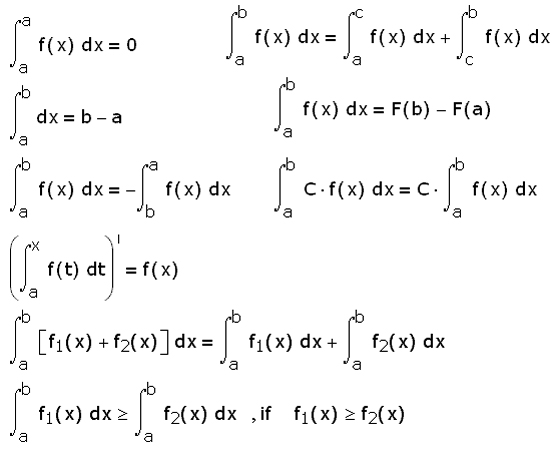
Определенный интеграл

Итак, интеграл -это некая сумма отдельных частей. Вот наиболее простые примеры для, более четкого понимания сути этого термина:

Предмет — это интеграл(сумма) молекул.
Лист в клетку — это интеграл(сумма) клеток.
Солнечная система — это интеграл(сумма) солнца и планет.
Общество — это интеграл людей.
Отрезок- это интеграл (сумма) метров. Если маленький отрезок, то сантиметров, миллиметров или микроскопических отрезков.
Площадь какой-либо поверхности — это интеграл квадратных метров, квадратных сантиметров или миллиметров, а также микроскопических площадей.
Объем- это интеграл кубических метров или, как их еще называют — литров.

Что такое определенный и неопределенный интегралы?

Начнем с определенного, так как его смысл поддается пониманию легче.

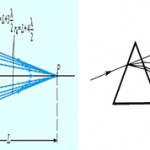
Геометрия изучает площади. Например, если вы хотите поклеить дома обои, вам надо знать площадь стен, чтобы узнать, сколько обоев вы должны купить. Тогда вы просто умножаете длину стены на высоту и получаете ее площадь. В данном случае, эта площадь является интегралом квадратных метров или сантиметров, в зависимости от того, в каких единицах вы ее измеряли. Но поверхности, площадь которых нам требуется вычислить далеко не всегда имеют форму прямоугольника, квадрата, или даже круга. В большинстве случаев — это сложные фигуры с волнистыми сторонами. Наиболее распространенный пример — площадь фигуры под кривой, имеющей уравнение y=1/x . Дело в том, что найти ее площадь при помощи обычных формул, которыми мы находим площадь квадрата, круга или даже сферы — невозможно. Для этой цели был разработан определенный интеграл.

Суть метода в том, что нашу сложную фигуру нужно разбить на очень узкие прямоугольники, настолько узкие, что высота каждых двух соседних практически равна. Ясно, что по сути, можно уменьшать толщину этих прямоугольников бесконечно, поэтому для обозначения их толщины используется размер dx. X — это координата, а приставка d — это обозначение бесконечно уменьшаемой величины. Поэтому, когда мы пишем dx — это значит, что мы берем отрезок по оси x , длина которого очень мала, практически равна нулю.

Итак, мы уже условились, что площадь любой фигуры- это интеграл квадратных метров или любых других фигур с более мелкими площадями. Тогда наша фигура, площадь которой мы ищем, представляет собой интеграл или сумму тех бесконечно тонких прямоугольников, на которые мы ее разбили. А ее площадь- это сумма их площадей. То есть вся наша задача сводится к тому, чтобы найти площадь каждого из этих прямоугольников, а затем их все сложить- это и есть определенный интеграл.

Теперь поговорим о неопределенном интеграле. Только, для того, чтобы понять, что это такое, сначала нужно узнать о производной. Итак, начнем.

Производная — это угол наклона касательной к какому-либо графику в какой-нибудь ее точке. Иными словами — производная — это то, насколько график наклонен в данном его месте. К примеру, прямая линия в любой точке имеет один и тот же наклон, а кривая- разный, но он может повторяться. Для вычисления производной существуют специальные формулы, а процесс ее вычисления называют дифференцированием. Т.е. дифференцирование — это определение угла наклона графика в данной точке.

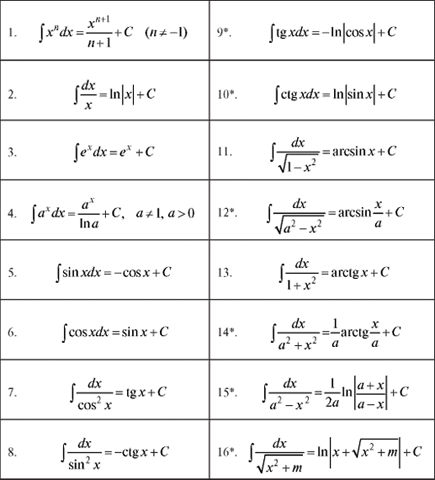
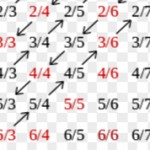
Таблица основных неопределенных интегралов

А для того, чтобы сделать наоборот — узнать формулу графика по углу ее наклона, прибегают к операции интегрирования, или суммирования данных обо всех точках. Интегрирование и дифференцирование- два взаимообратных процесса. Только здесь уже пользуются не тем интегралом, который был в первом пункте ( для определения площади ), а другим — неопределенным, то есть, не имеющим пределов.

Предположим, что нам известно, что производная некоей функции равна 5. 5 — это угол наклона графика к оси х в данной точке. Тогда, проинтегрировав производную, мы узнаем, что функция этой производной, которую еще называют первообразной — у=5х+с , где с- любое число. Для интегрирования, так же как и для дифференцирования есть специальные формулы, которые можно найти в таблицах.

Заключение

В заключение прорезюмируем, что основное отличие определенного интеграла от неопределенного — в их назначениях. Определенные интегралы используются для вычисления ограниченных параметров, таких как площадь, длина или объем, а неопределенный — при вычислении параметров, не имеющих границ, то есть функций.

Интересное видео на эту тему: